Diseño Geométrico: Trabajando Con Círculos

Ya hemos utilizado círculos ampliamente para crear varias cuadrículas para una serie de patrones. En esta lección estamos utilizando los círculos por su propio bien, es decir, en dos tipos de construcciones: espirales y círculos inscritos.

Espirales

Las espirales vienen en variados tipos diferentes. La distancia entre giros, y el ángulo de cada giro, determina su apariencia. Algunos se pueden definir usando una ecuación matemática, que se traduce, para las espirales específicas, en las construcciones geométricas fáciles - aproximadas, pero quizá lo bastante buenas para el ojo.

Espiral Regular o de Arquímedes

Esta espiral se define por una distancia igual entre giros, se dice que tiene un aspecto concéntrico. Se dibuja moviendo el punto de compás de un punto a otro en una figura de base que puede ser un segmento (dos puntos), un triángulo, un cuadrado, etc. Cuantos más puntos, más estrecha y más perfecta la espiral, pero también hace que la construcción sea más tediosa, por lo general un hexágono suele ser más.

Espiral Construida sobre Dos Puntos

Paso 1

En una línea horizontal, dibuja un semicírculo que sea lo más pequeño posible. Este es el primer giro de la espiral, y los dos puntos donde corta la línea son los puntos de construcción.

Paso 2

Coloque el compás en uno de los puntos, abra para encontrarse con el otro y dibuja un semicírculo al otro lado de la línea.  Los dos semicírculos forman una curva continua.

Paso 3

Mueva el compás al primer punto, ábralo para alcanzar el final de la curva y dibuja otro semicírculo.

Paso 4

Continúe en esta línea, moviendo el compás de uno de los puntos de construcción a la otra y ajustando la apertura cada vez para tomar las curvas donde lo dejaste.

Continúe así tanto como lo que desee. La espiral se verá así:

Espiral Construida sobre Tres Puntos

El método es el mismo pero comenzamos con un triángulo equilátero, cuyos lados se extienden. El compás se moverá del punto 1 al 2 al 3 y luego regresa al 1, y así sucesivamente. Si los lados se extienden como se muestra aquí, la espiral gira en el sentido de las agujas del reloj (y el compás se mueve de un punto a otro en el sentido de las agujas del reloj).

Paso 1

Dibuja el primer arco.

Paso 2

Muévase al siguiente punto, ajuste la apertura y dibuja el siguiente arco.

Paso 3

Muévase al tercer punto y repita.

Después de unos pocos giros, la espiral se ve así:

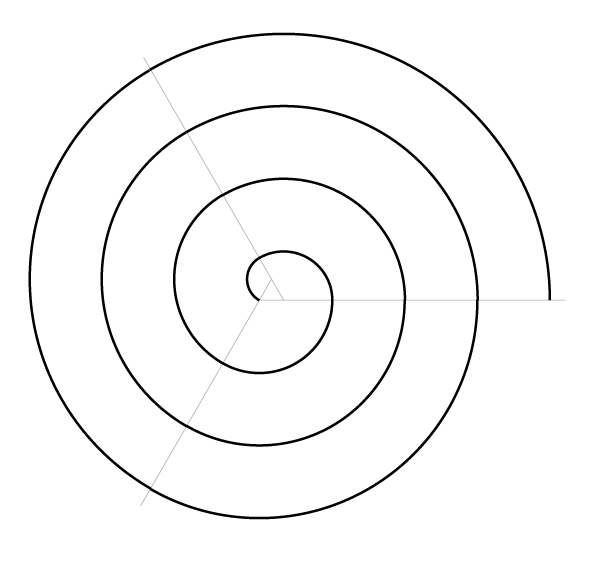
Espiral Construido sobre Cuatro Puntos

Nuestra base es ahora un cuadrado, y seguimos trabajando en el sentido de las agujas del reloj. A medida que el ángulo de los giros se hace más pequeño (primero fue 180º para cada uno, luego 120º, ahora 90º), la espiral se vuelve más suave.

Paso 1

Dibuja el primer cuarto de círculo.

Paso 2

Muévase al segundo punto, ajuste la apertura del compás y dibuja el siguiente cuarto de círculo.

Paso 3

Repita con los puntos tercero y cuarto.

Paso 4

Cómo luce la espiral después de algunas vueltas:

Espiral Construida sobre Seis Puntos

Con un hexágono como base, la construcción es realmente la misma. La parte crítica es dibujar las bases y la extensión de sus lados con mucha precisión. A continuación, sólo moverse a través de los seis puntos:

La espiral después de algunas vueltas:

Cuando estas espirales se colocan una al lado de la otra, podemos apreciar cuán suaves y perfectamente circulares son cuando la base tiene un mayor número de puntos.

Espiral Dorada

En contraste con las anteriores espirales regulares, la distancia entre giros sucesivos en espirales logarítmicas crece en una secuencia geométrica. Estas espirales, que se encuentran en el crecimiento de muchos organismos, son similares a sí mismas: el tamaño de la espiral aumenta, pero su forma no es alterada (por esto también fue llamada spira mirabilis, la "espiral milagrosa"). La espiral dorada es un tipo de espiral logarítmica con un factor de crecimiento vinculado al Número Dorado.

La manera más simple de dibujar tal espiral es partir de sus límites exteriores, contrariamente a la anterior. Por lo tanto, comenzaremos construyendo un rectángulo de dorado (explicaré qué es cuando esté realizado).

Paso 1

Construir un cuadrado.  (¿Olvidó cómo? Vea Trabajando con 4 y 8.)

Paso 2

Extienda los lados AB y DC.

Paso 3

Con la punta seca en E y el compás abierto a EC, dibuja un arco que corte el AB extendido en G.

Paso 4

Mueva la punta seca a F y dibuja un arco que corte el CD extendido en H.

Paso 5

Une a GH para completar el rectángulo.

Esto se llama un rectángulo dorado porque AB / AG = BG / AB, en otras palabras, la relación del lado más largo con todo el segmento es la misma que la del lado más corto al más largo.

Un ejemplar de papel A4 (o cualquier otro tamaño en la serie A) es un rectángulo dorado, así usted puede utilizar su superficie total como el rectángulo exterior, y vaya directamente al paso 6.

Paso 6

Ahora tenemos que desglosar este rectángulo dividiéndolo en cuadrados. Ya tenemos el primer cuadrado. El siguiente será sacado del rectángulo BGHC.

Coloque su punta seca en B y ábralo a la longitud del segmento corto. Marque I en BC.

Mueva la punta seca a G y marque J en GH.

Paso 7

Conectar IJ: ahora tenemos un cuadrado BGJI, y un nuevo rectángulo de sobra.

Paso 8

Repita esta operación en cada rectángulo sucesivo, siempre creando el cuadrado contra el borde exterior del rectángulo.

Cuando tenemos suficientes cuadrados, o son demasiado pequeños para trabajar, podemos dibujar la espiral apropiada.

Paso 9

Coloque la punta seca en C, deje que la abertura sea igual al lado del primer cuadrado y dibuja un cuarto de un círculo DB.

Paso 10

Mueva la punta seca a I, reduzca la abertura al lado del segundo cuadrado y dibuja un arco BJ.

Y así sucesivamente a través de todos los cuadrados...

La sensación de esta espiral es muy diferente de la apariencia concéntrica e incluso estática de las espirales regulares: es mucho menos contenida, con movimiento dinámico.

Círculos Inscritos

Los círculos pueden ser inscritos, es decir, dibujados dentro de una forma de tal manera que sean tangentes a sus lados, en ángulos, polígonos u otros círculos. Este recurso es la base de gran parte de la geometría decorativa de Occidente, por ejemplo, en la iluminación Celta o rosetones góticos. Veremos dos construcciones básicas que podemos utilizar con cualquier polígono o cualquier número de círculos dentro de un círculo, y luego construir dos ventanas completadas con su tracería.

Círculo en un Sector

Este método le permite ajustar el número de círculos de su elección dentro de un círculo. Comience dividiendo su círculo uniformemente en el número deseado de secciones, luego para cada sector proceda como sigue. El sector mostrado aquí es el de un círculo dividido en seis.

Paso 1

Bisectar el sector. La bisectriz corta el arco en Q.

Paso 2

Ahora necesitamos dibujar la perpendicular a PQ en Q. Con la punta seca del compás en Q, y cualquier abertura, dibuja un arco que corte la bisectriz en el punto A.

Paso 3

Mueva la punta seca a A y dibuja otro arco cortando el primero en B.

Paso 4

Conecte la línea AB y extiéndala un poco.

Paso 5

Con la misma abertura del compás y el punto en B, marque el punto C.

Paso 6

CQ es la perpendicular a PQ.

Paso 7

Extienda un lado del sector para cortar CQ en el punto E.

Paso 8

Bisectar el ángulo QEP.

Esta bisectriz corta QP en un punto O.

Paso 9

El punto O es el centro del círculo inscrito en este sector. Ahora se puede dibujar el círculo, con la punta del compás en O y la apertura ajustada en OQ.

Aquí están algunas posibilidades, dependiendo del número de sectores en los que se dividió el círculo. Observe que, siendo los círculos tangentes, los arcos entre sus puntos de contacto pueden omitirse para crear rosetas.

Círculo en una Cometa

Este método consiste en encajar un número de círculos en un polígono igual al número de lados de ese polígono (tres círculos en un triángulo, cinco en un pentágono, cuatro u ocho en un octágono ...).

Primero conecte el centro de cada lado al centro del polígono, dividiendo así el polígono en cometas, y proceda como sigue para cada cometa.

Paso 1

Bisectar ACB. Esta bisectriz corta AB en O.

O es el centro de nuestro círculo inscrito, pero para determinar con exactitud el radio del círculo, necesitamos encontrar un punto F en AD para que OF sea perpendicular a AD. Este es el propósito de los pasos restantes:

Paso 2

Con la punta seca en A y el compás abierto en AO, dibuja un arco.

Paso 3

Mueva la punta seca a D y repita, para encontrar el punto E.

Paso 4

Une a OE para cortar AD en F.

Paso 5

Ahora se puede dibujar el círculo inscrito, con el centro O y el radio OF.

Como con la construcción anterior, los diferentes polígonos resultarán lugar a formas diferentes, y los arcos interiores se pueden borrar para crear rosetones.

Ventana de Triskele (Tres Círculos)

Muchas ventanas de iglesia que dejan entrever una influencia Celta se pueden reconocer en muchos lugares alrededor de las islas británicas.

Paso 1

Comience con un círculo. Divídelo en seis partes y dibuja los diámetros.

Paso 2

Une tres de estos puntos para crear un triángulo equilátero.

Paso 3

Con el compás a una abertura menor, dibuja el círculo inscrito dentro del triángulo.

Paso 4

Dibuja otro triángulo, inscrito en este círculo.

Paso 5

Con el compás a una abertura menor, dibuja los tres círculos centrados en los puntos del triángulo.

Paso 6

Con el compás a una abertura inferior, dibuja el círculo en el cual están inscritas las tres más pequeñas.

Si sólo desea un renderizado lineal, puede detenerse aquí y entintar los siguientes arcos:

Para dibujar la tracería de la ventana, es decir, para dar a estas líneas su propio espesor y detalle, (donde la "línea", que es el marco de la ventana, tiene espesor y detalle propio), llevar a cabo ...

Paso 7

Coloque la punta seca sobre una de las intersecciones de un diámetro con el último círculo que dibujamos, y establezca la apertura a la diferencia entre los dos círculos grandes. Dibuja un pequeño círculo.

Paso 8

Vuelva a colocar la punta seca en el centro original y ábralo como se muestra. Dibuja un tercer círculo más profundo.

Paso 9

Ahora, para cada uno de los tres círculos, trace un círculo interno usando la abertura que se muestra a continuación.

Paso 10

Ahora cambia la abertura como se muestra, y para cada uno de los tres, dibuja este arco:

Paso 11

Ahora puedes entintar los dos círculos exteriores.

... luego las formas de gota interna...

... y finalmente las líneas centrales del triskele.

Ventana de Rosetón (Ocho Círculos)

Se trata de una ventana del frente Oeste de la catedral de Chartres, y la más antigua del edificio.

Paso 1

Comience con un círculo grande. Divídalo en ocho, siguiendo los pasos para dibujar un cuadrado (no hay necesidad de dibujar el cuadrado en sí, porque sólo necesitamos sus diagonales).

Paso 2

Corte la mitad de los sectores para dividir el círculo en 16.

Ahora hay ocho diámetros. Numere los puntos para mayor claridad.

Paso 3

Une los puntos pares para crear un octógono estático.

Paso 4

Los lados del octágono cortan los diámetros en ocho puntos. Únase a éstos para crear un octágono dinámico inscrito.

Paso 5

Ahora dibuje un octógono más estático inscrito en el anterior.

Paso 6

Ahora, volviendo a los puntos numerados, unir los siguientes pares: 2-8 y 10-16, luego 4-14 y 6-12.

Paso 7

Une a 2-12 y 4-10, y finalmente 6-16 y 8-14.

Observe los siguientes lugares donde se intersectan tres líneas: son los centros de los ocho círculos que forman la roseta.

Paso 8

Con el compás en una apertura menor, dibuja un círculo centrado en cada uno de estos puntos.

Entinta los arcos que se muestran aquí.

Paso 9

Cambie la apertura del compás como se muestra aquí, y repita. No hay necesidad de dibujar los círculos completos- se puede detener los arcos donde los diámetros se encuentran, y entintar de esa manera.

Paso 10

Cambie el compás una vez más y repita, deteniéndose de nuevo en los diámetros.

Paso 11

Une los extremos abiertos de los arcos.

Paso 12

Entinta las líneas entre arcos; Son porciones de los diámetros.

Paso 13

Con un último ajuste del compás, dibuja y entinta el círculo inferior.

Paso 14

Finalmente, entinta el círculo externo.

Con este capítulo sobre círculos, hemos completado la parte básica de estas lecciones sobre diseños geométricos.  A partir del próximo mes nos centraremos en patrones completos y motivos de creciente complejidad, tanto del Oriente como del Occidente.